Mathematical Model for the Public Campaign on Typhoid Fever Transmission and Control

Abstract

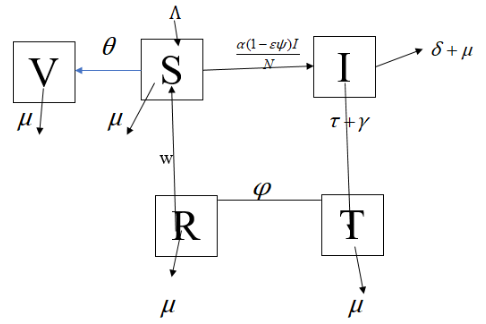
In this paper, we examined the dynamics of the typhoid fever model; in order to validate our model formulations and governing equations, we first established the disease-free equilibrium (DFE) of the state as well as the endemic equilibrium (EE). This paper further performed the local stability of the disease-free equilibrium. The basic reproductive number, R₀, is determined using the next generation matrix approach. finally, the paper demonstrated that, when R₀ < 1 is less than one, the disease-free equilibrium is considered to be globally asymptotically stable, and it guarantees that the disease will eventually be eradicated.